Diese Seite funktioniert nur mit Javascript.

Scitovsky-Indifferenzkurven
5.2.2 Große Nutzenmöglichkeitskurve
Soziale Wohlfahrtsfunktionen
W

Wir kennen bereits die Nutzenmöglichkeitskurve im Punktsinn als Übertragung sämtlicher Kombinationen der Nutzenniveaus auf der Kontraktkurve in den Nutzenraum. Der Namenszusatz "im Punktsinn" weist dabei auf die Konstruktion dieser Kurve für eine ganz bestimmte Gütermengenkombination, also einen Produktionspunkt hin. Da bei gegebener Faktorausstattung jedoch unendlich viele Produktionsmöglichkeiten bestehen, lassen sich ebenso viele Nutzenmöglichkeitskurven im Punktsinn konstruieren. Sinnvollerweise wählt man dabei unter den Produktionsmöglichkeiten nur die technisch effizienten aus, beschränkt sich also auf die (immer noch unendlich vielen) Punkte auf der Transformationskurve.

Abbildung 1
Die Große Nutzenmöglichkeitskurve ist die "nordöstliche Grenze" aller Nutzenmöglichkeitskurven im Punktsinn.

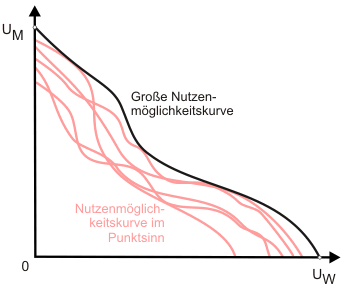
In Abbildung 1 sind einige dieser Nutzenmöglichkeitskurven eingezeichnet.

Die Umhüllende aller Nutzenmöglichkeitskurven im Punktsinn heißt Große Nutzenmöglichkeitskurve oder Nutzenmöglichkeitskurve im Situationssinn bezeichnet (utility possibility curve in the situation sense). 

Der Namenszusatz "im Situationssinn" deutet die Ableitung der Großen Nutzenmöglichkeitskurve als äußere Grenze der individuellen Nutzenkombinationen für eine Situation gegebener Nutzenfunktionen und Faktorausstattung an. Nach wie vor besteht jedoch keine Möglichkeit der kardinalen Nutzenmessung, so dass über die Gestalt der Kurve nicht mehr gesagt werden kann, als dass sie monoton fallend verläuft: In einer Volkswirtschaft, die sich auf der Großen Nutzenmöglichkeitskurve befindet, ist eine Verbesserung im Sinne des Pareto-Kriteriums ausgeschlossen.

Um die Eigenschaften von Nutzenmöglichkeitskurven noch etwas genauer zu untersuchen, betrachten wir die Scitovsky-Indifferenzkurven in Abbildung 2.

Da auf einer Scitovsky-Indifferenzkurve die Nutzen der Individuen konstant sind, entspricht eine Scitovsky-Indifferenzkurve einem Punkt im Nutzenraum. (Umgekehrt gilt für Nutzenmöglichkeitskurven, dass ein Punkt im Güterraum einer Kurve im Nutzenraum entspricht.)
Abbildung 2
Scitovsky-Indifferenzkurven im Güterraum können sich schneiden.

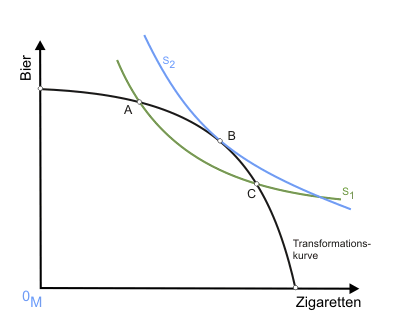
Da nun zugleich eine Scitovsky-Indifferenzkurve alle alternativen Gütermengen repräsentiert, die zur Erzielung der durch sie bestimmten Nutzenniveaus gerade notwendig sind, schneiden sich die Nutzenmöglichkeitskurven der Punkte A und C in dem "Scitovsky-Indifferenzpunkt" der Kurve S1 im Nutzenraum. Dieser Punkt kann demzufolge nicht auf der Großen Nutzenmöglichkeitskurve liegen. Mit der analogen Überlegung bestätigt man den Punkt B ( die Grenzrate der Substitution ist hier gleich der Grenzrate der Transformation) mit der Scitovsky-Indifferenzkurve S2 als Bestandteil der Großen Nutzenmöglichkeitskurve. Qunitessenz:

Ein Allgemeines Gleichgewicht ist im Nutzenraum immer ein Punkt der Großen Nutzenmöglichkeitskurve. 

Eine Bewegung in nordöstlicher Richtung im Nutzenraum kann eine Volkswirtschaft nur von Punkten aus realisieren, die unterhalb der Nutzenmöglichkeitsgrenze liegen. In diesen Punkten wurde entweder

  1. 1. nicht tauschoptimal verteilt,
  2. 2. nicht effizient produziert oder
  3. 3. die Produktion nicht den Konsumwünschen angepasst.
 

Jetzt, wo wir wissen, was eine Gesellschaft bei gegebenen Ressourcen und dem in Produktionsfunktionen verkörperten technischen Wissen an Nutzen hervorbringen kann, wenn technisch effizient produzierte Gütermengen optimal verteilt werden - wenn wir also die Restriktion kennen -, besteht offensichtlich das entscheidende Problem darin, einen der Punkte auf der Großen Nutzenmöglichkeitskurve als gesellschaftliches Optimum auszuwählen. Will man deutlich machen, dass nur wirtschaftliche Größen betrachtet werden, kann man auch von einem gesamtwirtschaftlichen Optimum sprechen. 

Um einen Optimalpunkt zu ermitteln, bedarf es einer Regel, die zwischen den Punkten der Großen Nutzenmöglichkeitskurve diskriminiert. Das Pareto-Kriterium beispielsweise reicht dafür nicht aus, da ja alle diese Punkte pareto-optimal sind. Dieses Kriterium lässt uns also bei der Frage nach der Verteilung der Nutzen in einer Gesellschaft - d. h. indirekt bei der Frage nach der personellen Einkommensverteilung - im Stich. 

Bevor wir nun ein Instrument einführen, mit dessen Hilfe auch Distributionsfragen angegangen werden können, ist darauf hinzuweisen, dass sich an dieser Stelle eine Erörterung der sogenannten Kompensationskriterien anböte. Diese Kriterien (die bekannteren stammen von Kaldor, Hicks, Scitovsky und Samuelson und tragen auch deren Namen) sind allesamt entwickelt worden, um im Vergleich zum Pareto-Kriterium zu weitergehenden Aussagemöglichkeiten bezüglich der Wünschbarkeit gesellschaftlicher Situationen zu kommen. Alle diese Kriterien sind wie das Pareto-Kriterium Werturteile und alle können die in sie gesetzten Erwartungen entweder nicht oder nicht zufriedenstellend erfüllen. Hier kann jedoch auf die Kompensationskriterien nicht näher eingegangen werden - für den weiteren Gang der Argumentation ist das aber auch nicht unbedingt erforderlich.

 
|           | Impressum